低成本3D打印和CNC铣床机具推陈出新，让更多业余爱好者在自己家里，也能设计并制作复杂的零件，但光凭这些技术并不够，以致聚乳酸（PLA）或高密度聚乙烯（HDPE）塑料所制成的功能性原型，其硬度和强度皆差强人意。

     大家面对这个问题，凭直觉就是扩充零件的规模和数量，却也增加了打印时间和材料成本，牺牲了整体效用和美感表现。既然这个解决方案令人难以忍受，部分自造者开始诉诸更昂贵或更困难的材料，例如铝或聚醚醚酮（PEEK）。

事实上，这些烦恼大多可以避免。制造业老想着节省时间和金钱，早就研发出一些简单的招数，以便应付最难搞的材料，达到他们心目中的标准。本文介绍一下基本工程概念，以及这些概念如何落实于零件设计。

神奇的弯曲世界

日常工程材料五花八门，端视会如何受到挤压、拉扯、弯曲和使用而定。说到小型机械原型，有一项特征最为重要：承受弯曲的能力。

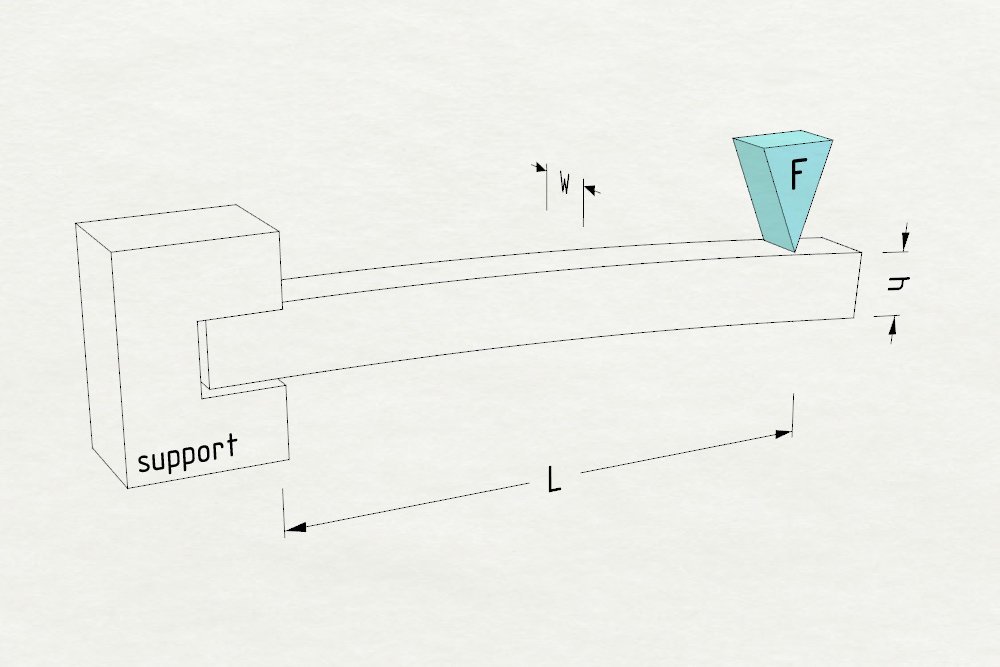
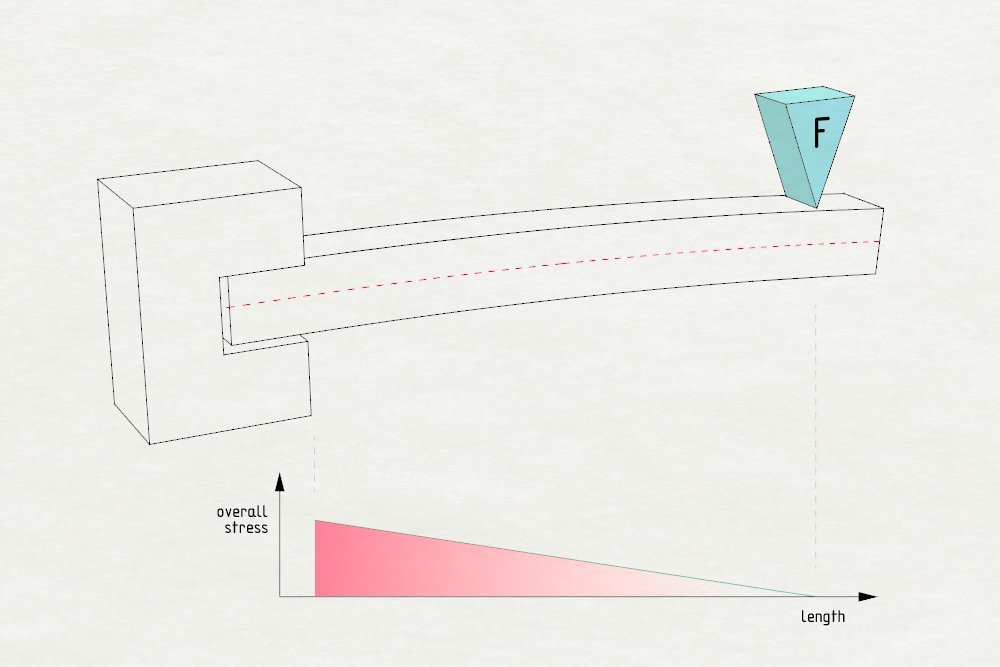
为什么零件受到弯曲会损坏？我们试想一个很常见的简单情境：长方形横木一端卡住，另一端承受弯力(F)。

弯曲横木

依照常识判断，横木承受弯力之后，上表面原子彼此分离，被压缩到另一侧。若弯力持续加大，这些分子所承受的压力也会增加，甚至超过把一切凝聚起来的电磁力。每一种材料都有固定的承压临界点，但仍取决于有多少分子，分子排列成什么形状而定。

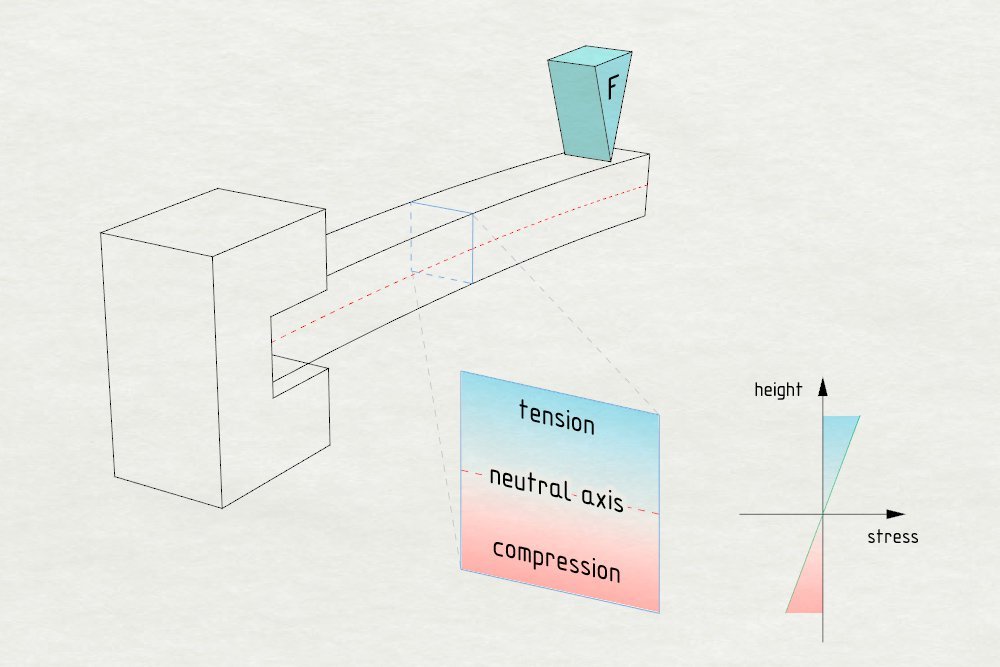
最后会怎么样呢？首先，就我们所知，横木的外表面承受最大的张力和压缩力，压力也会是最大。简单来说，那些区域之间会线性转移，进而在横切面的中央，形成不受压力的中轴。

弯曲压力分布，观察长方形横木的横剖面

我们看这个二维横剖面图，中轴总是跟施力方向垂直。若是长方形等对称形状，中轴会贯穿横木的中央，至于其他几何形状，中轴则会贯穿质心，亦即几何形状的质量中心，任何CAD软件皆可自动辨识质心的位置，网络上也能轻易找到符号公式和计算器。

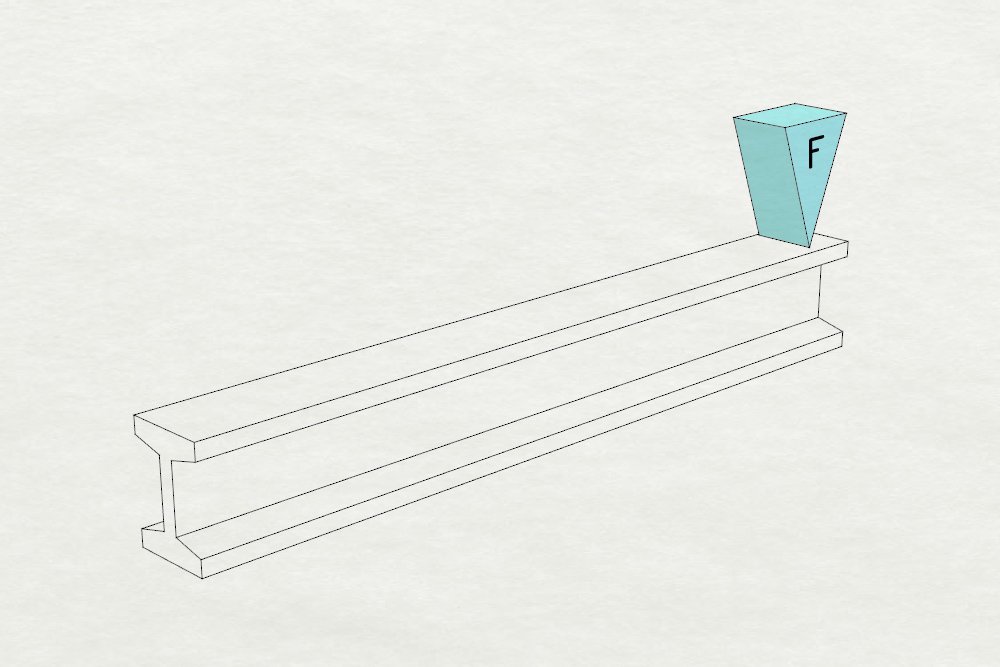
位于横木中央的低压力区，就很值得我们思考：搞不好可以从那里挖走一些材料，用来强化外表面的高压力区，一来提高坚韧度，二来却不会增加重量。这绝非天马行空的狂想，这正是工字梁的运作原理。

在建筑业，若工字梁和矩形梁使用等量的钢材，工字梁的表现出色不少，但缺点是容易扭曲、变形和折断，尤其是中央区域太薄的情况下

然而，我们也别好高骛远，说到压力分布，有一件事千万不要忘了：只要横切面连续不断，横木就相当于简易的杠杆，弯曲力矩跟施力和有效距离成比例，于是横木所承受的整体压力，也会随着长度而改变，从零开始直线上升到定锚点。

综合目前为止的两项观察，我们可以推论最大的压力，集中在横木的特定区域：也就是定锚点旁边的外表面。把这一点谨记在心，我们试着厘清在什么条件之下，这股压力会超过材料的承受范围。

计算弯曲的压力

为了计算最大承受压力，以下是有实验支持的公式：

σmax=F*L* cx / Ix

我们试着拆解这个公式：靠近定锚点的表面压力，似乎跟施力(F)和横木有效长度(L)的交乘成比例。除此之外，这也跟横木最外围和中轴的距离（cx）成比例，长方形横木cx相当于h / 2。一切昭然若揭。

更重要的是，这股压力也跟截面矩（Ix）成反比，截面矩正是以量化呈现材料相对于中轴的分布，指出施力会对抗多少分子，分子会承受多大的拉力。为这个参数导出公式，必须先解出某个积分，但CAD软件通常会自动找出特定数值，若没有CAD软件，在线计算器也会针对常见横木几何图形提供数值。

矩形横木截面矩公式如下，只需带入高度（h）和宽度（w）：

Ix = w * h3 / 12

综合这些方程式，下列为矩形横木最大承受压力：

σmax = 6 * F * L / (w * h2)

事实上，常见材料的供应商通常会进行标准弯曲测试，来计算自家产品的σmax ，这个数值在产品标示会写成抗弯强度，既然我们都知道σmax 数值，这时候只要解出F数值，我们就会知道为大承压能力，公式如下：

Fbreak = σmax * Ix / (L * cx)

如果带入矩形横木的Ix 和cx，得到新的方程式如下：

Fbreak = ⅙ * w * h2 * σmax / L

我们实际找个例子：假设有一片压克力板，宽度1公分，厚度3公厘，长度10公分，搜寻一下就知道抗弯强度为110MPa（亦即110,000,000 N/m2或 110 N/mm2），接下来就是算数了：

Fbreak = ⅙ * 10 mm * (3 mm)2 * 110 N/mm2 / 100 mm = 16.5 N ≈ 1.68 kgf

这样看起来，横木最大承受压力不超过1.6kgf，安全边际根本无足挂齿，若你使用聚苯乙烯（抗弯强度为40 MPa），最大承受压力只剩下0.6kgf，令人堪忧。

(责任编辑：admin)

• Cura第一层设置：初始层
• 一文了解3D打印水凝胶
• 珠宝如何3D打印？终极指南
• 蜡材料如何3D打印：终极指
• 如何制作防水3D打印件？
• 必看！3D打印支撑–终极指

• · Cura第一层设置：初始层简单解释
• ·一文了解3D打印水凝胶
• ·珠宝如何3D打印？终极指南来了，请收好
• ·蜡材料如何3D打印：终极指南来了，请收
• ·如何制作防水3D打印件？
• ·必看！3D打印支撑–终极指南
• ·6种从床上去除3D打印件的方法！
• ·2023年10款最适合初学者的免费3D建模软